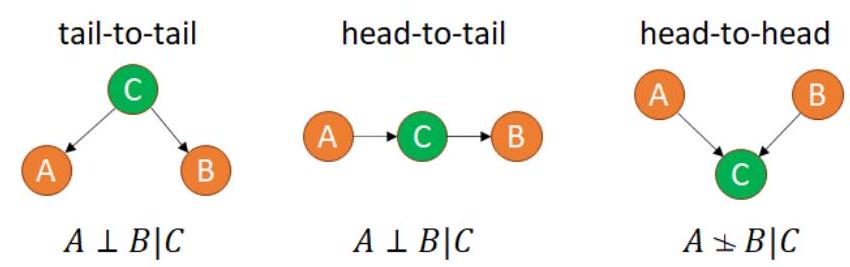
Linear Models

from pgmpy.models import BayesianNetwork # BayesianModel in old versions of pgmpy
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
import networkx as nx
import matplotlib.pyplot as plt
# Define the Bayesian model structure using edges
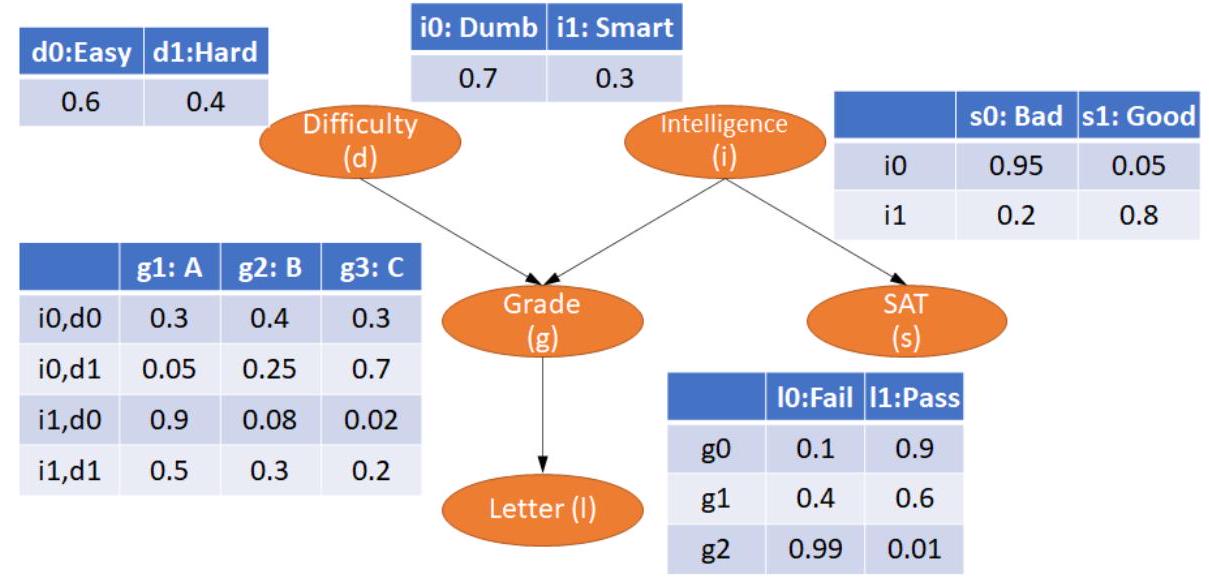
model = BayesianNetwork([('D', 'G'), ('I', 'G'), ('G', 'L'), ('I', 'S')])
#-----------------------Enter probabilities manually -----------------------------------
# Define CPD
cpd_d = TabularCPD(variable=' D', variable_card=2, values=[[0.6], [0.4]])
cpd_i = TabularCPD(variable='I', variable_card=2, values=[[0.7], [0.3]])
cpd_g = TabularCPD(variable='G', variable_card=3,
values=[[0.3, 0.05, 0.9, 0.5],
[0.4, 0.25, 0.08, 0.3],
[0.3, 0.7, 0.02, 0.2]],
evidence=['I', 'D'],
evidence_card=[2, 2])
cpd_l = TabularCPD(variable=' L', variable_card=2,
values=[[0.1, 0.4, 0.99],
[0.9, 0.6, 0.01]],
evidence=['G'],
evidence_card=[3])
cpd_s = TabularCPD(variable='S', variable_card=2,
values=[[0.95, 0.2],
[0.05, 0.8]],
evidence=['I'],
evidence_card=[2])
# Correlate DAG with CPDs
model.add_cpds(cpd_d, cpd_i, cpd_g, cpd_l, cpd_s)
#-----------------------------------------------------------------------------------------
model.get_cpds()
# Check the CPDs of different nodes
for cpd in model.get_cpds():
print("CPD of {variable}:".format(variable=cpd.variable))
print(cpd)
# Check the network structure and CPDs: valid if the total of CPD equals 1
model.check_model()
# Plot the Bayesian network
nx.draw(model,
with_labels=True,
node_size=1000,
font_weight='bold',
node_color=' y',
pos={"L": [4, 3], "G": [4, 5], "S": [8, 5], "D": [2, 7], "I": [6, 7]})
plt.text(2, 7, model.get_cpds("D"), fontsize=10, color='b')
plt.text(5, 6, model.get_cpds("I"), fontsize=10, color='b')
plt.text(1, 4, model.get_cpds("G"), fontsize=10, color='b')
plt.text(4.2, 2, model.get_cpds("L"), fontsize=10, color='b')
plt.text(7, 3.4, model.get_cpds("S"), fontsize=10, color='b')
plt.title('test')
plt.show()
from pgmpy.models import BayesianNetwork
from pgmpy.factors.discrete import TabularCPD
from pgmpy.inference import VariableElimination
import networkx as nx
from matplotlib import pyplot as plt
from pgmpy.estimators.MLE import MaximumLikelihoodEstimator
import numpy as np
import pandas as pd
raw_data = np.random.randint(low=0, high=2, size=(1000, 5)) # Create data using random numbers
data = pd.DataFrame(raw_data, columns=["D", "I", "G", "L", "S"])
# Define the Bayesian model structure using edges
model = BayesianNetwork([('D', 'G'), ('I', 'G'), ('G', 'L'), ('I', 'S')])
#----------------------Generate probabilities from data -------------------------------
# Obtain the parameters (CPDs) by fitting the model to the data
model.fit(data, estimator=MaximumLikelihoodEstimator)
model.get_cpds()
# Check the CPDs of different nodes
for cpd in model.get_cpds():
print("CPD of {variable}:".format(variable=cpd.variable))
print(cpd)
import pandas as pd
import numpy as np
from pgmpy.estimators.StructureScore import BDeuScore, K2Score, BicScore
from pgmpy.models import BayesianNetwork
# Generate samples using random numbers: there are 3 variables, in which Z depends on X and Y
data = pd.DataFrame(np.random.randint(0, 4, size=(5000, 2)), columns=list('XY'))
data['Z'] = data['X'] + data['Y']
bdeu = BDeuScore(data, equivalent_sample_size=5)
k2 = K2Score(data)
bic = BicScore(data)
# Method 1: Exhaustive Search
from pgmpy.estimators import ExhaustiveSearch
es = ExhaustiveSearch(data, scoring_method=bic)
best_model = es.estimate()
print(best_model.edges())
print("\nAll DAGs by score:")
for score, dag in reversed(es.all_scores()):
print(score, dag.edges())
# Method 2: HillClimbSearch
from pgmpy.estimators import HillClimbSearch
hc = HillClimbSearch(data)
best_model = hc.estimate(scoring_method=BicScsore(data))
print(best_model.edges())