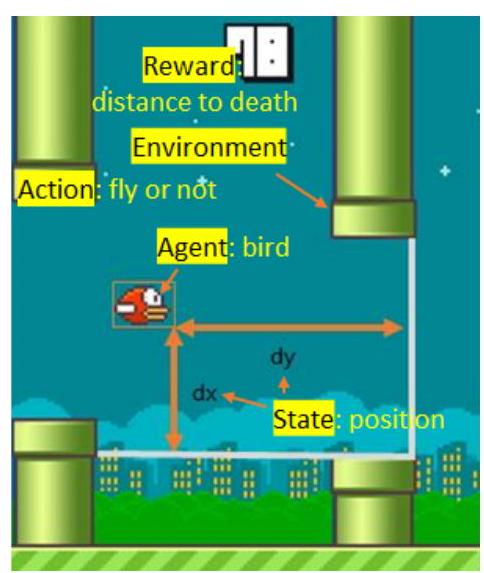
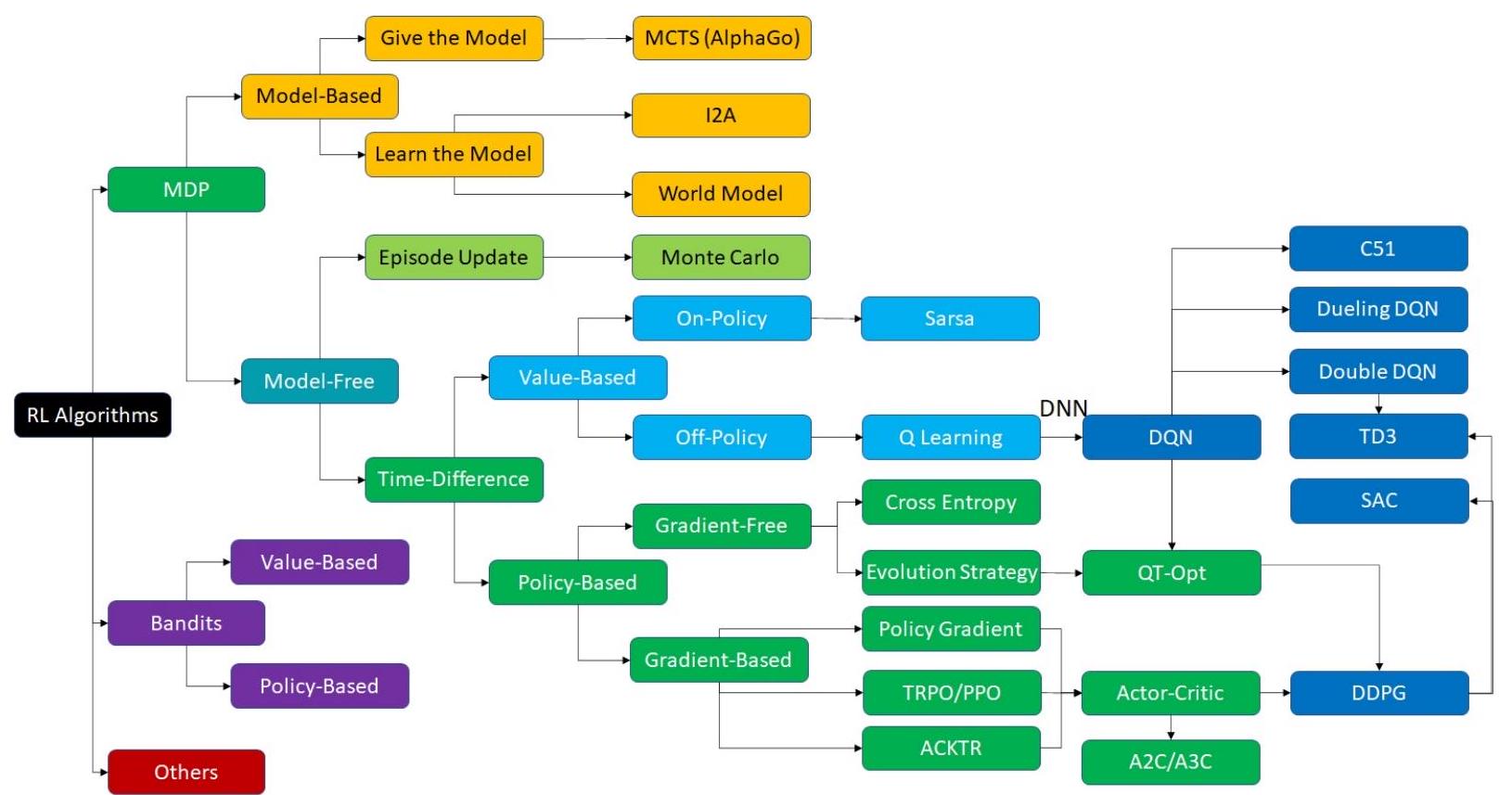
Linear Models

import numpy as np
import gymnasium as gym # Old versions use "import gym"
# Initialization
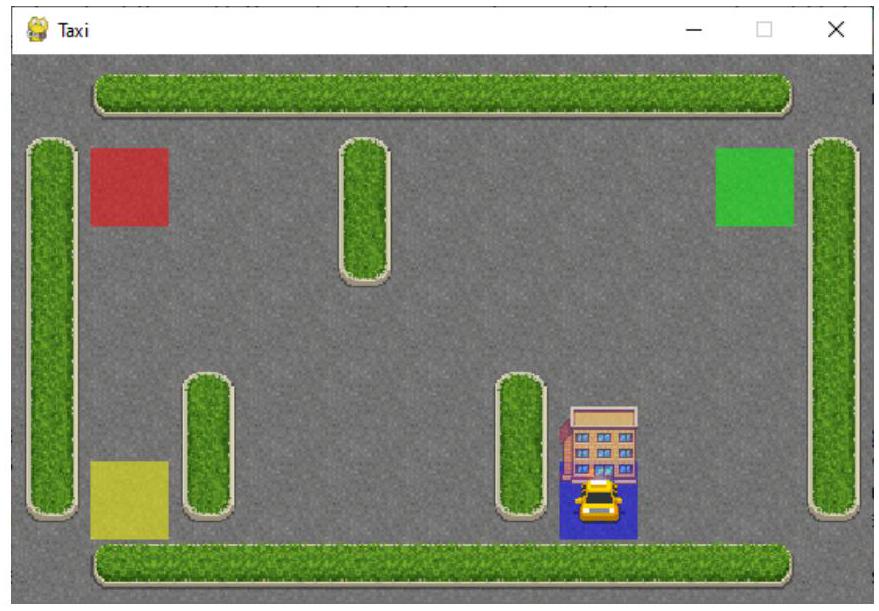
env = gym.make("Taxi-v3", render_mode="human") # Call the "Taxi-v3" environment from gym with the
name "env"
action_size = env.action_space.n # Obtain the size of the action space: how many actions. There are
six here
state_size = env.observation_space.n # Obtain the size of the state space: 5 rows * 5 columns * 5
passenger positions * 4 destinations =500 states
# Update state
state_new, reward, done, _, _ = env.step(action)
# Stop an episode when the environment tells an episode ends
if done == 1:
print('This is the #%i training episode' % n)
break
# Testing
state = env.reset()[0]
while True:
# Choose an action based on the Q table only
action = np.argmax(Table[state]) # Choose an action based on the Q table
state, reward, done, _, _ = env.step(action)
env.render() # Green is passenger; Red is destination
if done == 1:
break
import numpy as np
class treasure1D:
def ___init__(self,N):
self.n_cell = N # The greater this number, the higher n_episode is needed
self.Reward = np.zeros(self.n_cell);
self.Reward[-1]=1.0 # n_cell cells, only the rightmost has reward (end of game)
self.States = range(self.n_cell)
self.state = np.random.choice(self.States)
self.reward = 0
self.done = False
self.observation_size = 1 # Number of elements in observation (there is only one in this env
: state/position)
def reset(self):
self.state = np.random.choice(self.States)
self.reward = 0
self.done = False
return self.state
def step(self,action):
# Update state
reward = 0
if action == 'left' or action == 0:
if self.state == self.States[0]: # Leftmost
state_new = self.state # Does not move
self.done = True
self.reward = -10
else:
state_new = self.state - 1 # Obtain new state s^prime
else:
if self.state == self.States[-1]: # rightmost
state_new = self.state # Does not move
self.done = True
self.reward = 10
else:
state_new = self.state + 1 # Obtain new state s^prime
self.state = state_new
return self.state, self.reward, self.done, []
def render(self):
print ("The state is ", self.state, "The reward is ",self.reward)
import numpy as np
import pandas as pd
import gym
# Initialization
env = gym.make("Taxi-v3") # Call the "Taxi-v3" environment from gym with the name "env"
action_size = env.action_space.n # Obtain the size of the action space: how many actions. There are
six here
state_size = env.observation_space.n # Obtain the size of the state space: 5 rows * 5 columns * 5
passenger positions * 4 destinations =500 states
Table = np.zeros((state_size, action_size)) # Initialize the Q table
# Hyperparameter
epsilon = 0.9 # Parameter for epsilon-greedy
alpha = 0.1 # Learning rate
gamma =0.8 # Decay of rewards
# Training
n_episode = 10000 # Number of episodes for training
for n in range(n_episode):
state = env.reset() # Initialize the environment for each episode
while True:
# Choose an action based on the Q table with epsilon greedy
action_Q = np.argmax(Table[state]) # Choose an action based on the Q table
action_greedy = np.random.choice(Table[state].size) # Choose an action randomly for use in
the epsilon-greedy method
action = np.random.choice([action_Q,action_greedy],size=1,p=[epsilon,1-epsilon])[0]
# Update state
state_new, reward, done, _ = env.step(action)
# Update the table
Table[state,action] = (1-alpha)*Table[state,action] + alpha*(reward+gamma*max(Table[
state_new]))
# Prepare for the next step
state = state_new
# Stop an episode when the environment tells an episode ends
if done == 1:
print('This is the %i the episode' % n)
break
# Testing
state = env.reset()
while True:
# Choose an action based on the Q table only
action = np.argmax(Table[state]) # Choose action based on Q table
state, reward, done, _ = env.step(action)
env.render() # Green is passenger; Red is destination
if done == 1:
break